Работаем с данными

Количественные данные (числа) можно представлять в виде графиков и диаграмм, так их легче сравнивать, обсуждать и обдумывать. Диаграммы бывают разных типов. Три основных типа: столбчатая, круговая и график рассеивания

 

Столбчатые диаграммы

Они выглядят, как несколько прямоугольников равной ширины, высота которых отражает какое-то определенное число или значение.

Пример: В классе D - 45 учеников, это самый большой класс, а в классе В - всего 14 учеников, он меньше всех. Сколько учеников в классе F? ____________

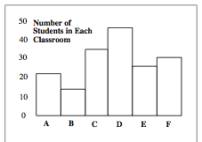
Классы

 

На вертикальной оси: Число учеников в каждом классе

На горизонтальной оси: Классы

В этом примере учеников легко было сгруппировать по классам, но как быть с данными, сгруппировать которые не так просто?

 

 

 

Возьмем значения температуры. В диаграмме можно отразить точные значения измерений, но это не даст особо интересной информации. Зато отдельные измерения температуры можно сгруппировать, объединить внутри определенных диапазонов. Каждый прямоугольник соответствует диапазону температур Каких температур нет на диаграмме? ______________

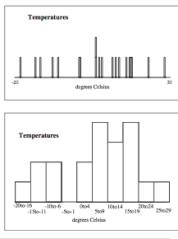
ература

 

Градусы Цельсия

 

На сайте <http://enlvm.usu.edu/ma/nav/bb_dlib.jsp> можно «поиграть» с СТОЛБЧАТЫМИ диаграммами.

 

Круговые диаграммы (или секторные диаграммы)

 

 

Секторная диаграмма – это круг, поделенный (словно пирог на куски) на сектора, соответствующие частям целого. На первой диаграмме представлен целый день одного человека. Половину (50%) дня этот человек спит; четверть (25%) проводит в школе; 10% времени он играет; 8% дня делает уроки; 7% времени проводит за едой.   На такой диаграмме разные сектора важны именно как части целого. Сектора указывают на процентное соотношение, а не абсолютные цифры Благодаря этому свойству круговые диаграммы помогают сравнивать данные двух или разных групп, в которых общее количество (целое) не совпадает. На следующих двух диаграммах – другой пример: это воображаемая школа, где половина учеников – мальчики, половина – девочки (диаг. 2). В одном классе этой школ, однако, девочек больше. Шесть из каждых 10 учеников там – девочки. Эти диаграммы можно сравнивать, хотя на одной представлены все ученики целой школы, а на другой – только одного класса. Число учеников не имеет значения. Важно лишь процентное соотношение.   На сколько процентов отличается относительное количество девочек в классе от их относительного количества в о всей школе? ________________________   На сайте <http://enlvm.usu.edu/ma/nav/bb_dlib.jsp> можно «поиграть» с такими диаграммами.

PIE CHARTS (above)

На таких графиках одна переменная (например, температура на участке ) наносится относительно другой переменной (например, высота). Два показателя связаны; они представляют собой пару.   Итак, оценим связь температуры и высоты; в целом, чем больше высота, тем ниже температура. Наш график может выявить такую взаимосвязь. Однако эта взаимосвязь не абсолютна, ведь на температуру могут влиять и другие факторы помимо высоты. Поэтому точки рассеяны.   Точки соответствуют парам (X,Y), в нашем примере – высоте и температуре.   Растет или падает температура с увеличением высоты? ___________________________ На сайте <http://enlvm.usu.edu/ma/nav/bb_dlib.jsp> можно "поиграть" с подобными схемами.

Графики рассеивания

(below)