Spherical Earth and Flat Maps - by George Collison

Aristotle's discovery that the earth was a sphere presented problems for later map-makers (cartographers). Maps are flat, after all, not round. Making a flat map of a sphere must introduce some distortion of the underlying land -- some become too large, some too small.

Cylindrical Map Projection

There are many mathematical projections of the sphere onto a flat surface. A common way is to project the sphere of the earth onto a cylinder. The map-maker imagines the earth is a transparent sphere inside a cylinder with a light at the center of the transparent sphere. The shadows of the parallels and meridians trace the projection on the cylinder. The cylinder is unrolled to make the cylindrical projection of the earth. Polar regions are cut off because they are too far from the equator.

The cylindrical projection is accurate around equatorial regions but it has many disadvantages in polar areas. The poles are at an infinite distance. Areas at high parallels, Russia, Canada , Alaska or Greenland appear much larger than they really are. Antarctica has an infinite area in a cylindrical projection. The cylindrical projection does not preserve area, nor compass direction. Parallels are parallel, but all meridians are also parallel; they never meet at the poles.

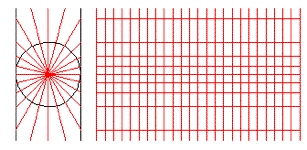
Cylindrical Map Projection

Another projection first made by Mercator, a Flemish cartographer about 1560 AD, is another kind of cylindrical projection. To make the Mercator projection the cartographer imagines a spherical earth expanding at a constant rate inside the cylinder. When the surface of this expanding sphere touches the cylinder it sticks. The cylinder is cut vertically and then unrolled.

The Mercator projection produces less distortion at high latitudes. It does not preserve relative areas; northern lands like Russia, Greenland, Canada, or Alaska, which appear larger than they really are. Meridians, as in a cylindrical projection, are also improperly displayed as parallel vertical lines. The polar regions are not shown. The Mercator projection does have one valuable property very useful for navigators. It preserves compass direction. The compass direction between two points on a Mercator projection is the same as the compass direction between the points on the sphere.

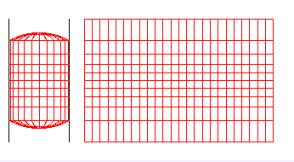
Mercator Map Projection

Robinson projection.

There are many other projections, each designed to reduce distortions in either area, compass direction, or distance. No flat projection is totally satisfactory. A common modern projection is the Robinson projection first published in 1974 in National Geographic. It is a complex hybrid cylindrical projection that is relatively accurate in presenting areas at most latitudes. Parallels are parallel, but meridians are ellipses of different sizes, approximately evenly spaced. Distances between points are relatively accurate. Poles are shown as lines, not points. Compass directions between points are not accurate.

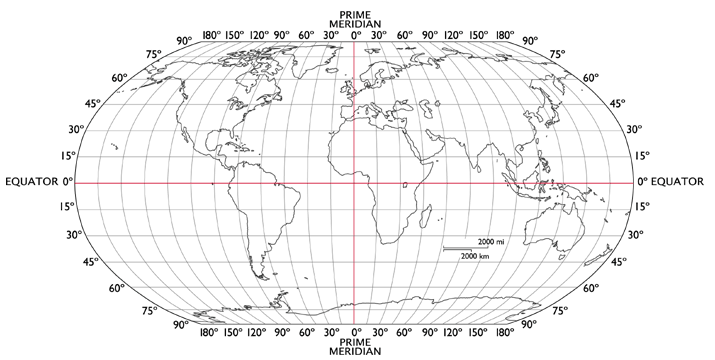
Robinson Projection.

Exercises to confirm understanding.

A. Make a table that describes the three different projections discussed in this reading, Cylindrical, Mercator, and Robinson.

B. Describe how parallels and meridians are shown in each projection. Note how areas are represented and any distortions that the projection introduces. Note how the polar regions are show in that projection. Note the accuracy of distances between two points.

Joining Global Lab ll GL Activities (English) Index ll Russian/English GL Home