Significant Digits

1. All measurements have some limit to their precision. You can only be as precise as the instrument used to make the measurement.
2. The digits which are considered significant are all the measured digits plus one estimated digit. How many significant digits were there in each of the measurements I made with the various rulers during the demonstration?
3. Here are some rules to help determine how many significant digits are in a number
   1. All non-zero digits should be counted. (ex. 432.181 has 5 significant digits)
   2. Zeros to the left of non-zero digits are never counted. (Ex. 0.000456 has 3 significant digits)
   3. Zeros to the right of non-zero digits definitely count if a decimal place is present and may or may not count if a decimal place is not present.
      • The number 11.5000 has 6 significant digits.
      • The number 11000 could have between 2 and 5 significant digits. This is ambiguous because you don't know how this measurement was made. Perhaps it is only an estimate good to the thousands place. Then there would be only 2 significant digits.
4. In the last example, where the number 11000 has an ambiguous number of significant digits, scientific notation will clear up this problem. 11000 can be written several ways in scientific notation to indicate a certain amount of significant digits.

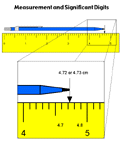
   1.10 x 104	=	11000	and has 3 significant digits.
   1.1 x 104	=	11000	and has 2 significant digits.
   1.1000 x 104	=	11000	and has 5 significant digits.

5. Try counting the significant digits in following set of numbers

   3.456	5.000	10003
   0.666	5.001	0.00300
   5	0.005	314.000
   10000	12000	10000.0
   100321	90210	314000

   see answers below
   
   For more significant digit practice go to: http://brad.tcimet.net/java_samples/sigfigs/autogen_SigFigs.html
6. Significant digits in calculations - see the handout Calculations With Significant Digits for examples.
   1. Addition/Subtraction - you examine the decimal places of each of the numbers to determine the number of decimal places in the final answer. The final answer should be rounded to the same number of decimal places as the number with the least number of decimal places used in the calculation.
   2. Multiplication/Division - you examine all the significant digits of each of the numbers to determine the number of significant digits in the final answer. The final answer should be rounded to the same number of significant digits as the number with the least significant digits used in the calculation.
   3. You can find an applet written to help you practice doing cacluations here.

previous page

chemsite homepage

The numbers which are in bold are definitely significant. The green numbers may or may not be significant depending on how the measurement was made.

previous page

chemsite homepage